I start by saying that this is certainly an opinion piece. However it’s not just pure opinion. My opinion on this subject is backed by a mathematical analysis of hashing algorithms. There are certainly some complicating factors that may be argued to influence the described scenario in all reality. However, given that I believe the core logic holds, a strong argument may be made against the use of B/S-crypt.
If you aren’t already aware, as to what Bcrypt and Scrypt are, a brief explanation follows. BCrypt is a computationally difficult algorithm designed to store passwords by way of a one-way hashing function. You input your password to the algorithm and after significant (relative) computation, an output is produced. Bcrypt has been around since the late 90s and has handled significant scrutiny by the information security/cryptography community. It has proven reliable and secure over time.
Scrypt is an update to the same model from which Bcrypt arose. Scrypt is designed so as to rely on high memory requirements as opposed to high requirements on computational power. The realization that lead to this, was that specialized computer chips (FPGA/ASICs/GPUs) could be purchased at scale by an attacker easier than could huge amounts of memory for a traditional computer.
The goal for both of these algorithms is the same. To attempt to make it harder to run the algorithm. If an attacker wishes to brute force any given plaintext password -> given only a password hash; he must guess plaintexts, compute the hash of that plaintext then compare the output (the hash of his guess) with the known stored password hash. (Ex. Attacker captures hash_0; must guess A for A in all guesses until hash(A) = hash_0.)
As you can see by the above. If the password is hard to guess, then the attacker must run the algorithm a massive amount of times to be able to find the correct input to the algorithm which will match the stolen hash value on output. Therefore, the idea behind BCrypt and Scrypt is to increase the amount of time it takes the attacker to make any single guess, and by extension massively increase the time it takes him to find the correct answer.
There is actually an issue here though. Fundamentally, the idea that BCrypt and Scrypt are solutions is built on a faulty premise. People want to feel safe. It makes sense that any idea which could potentially be seen to offer businesses hope that their stored passwords will not be cracked in the event of a breach would be particularly compelling.
But right off the bat, there is a real problem with Bcrypt and Scrypt. By requiring extensive computation to process a logon event, they increase the load on a company’s server resources; stealing from business critical applications just to play around with math on the off chance that one day the stored passwords are stolen.
But not only are Bcrypt and Scrypt wasting server resources on an ongoing basis; regardless of any reality to the threat against a given service… they aren’t even the most logical response to the issue presented by contemporary password storage dilemmas.
There is a function that can be used to describe the time it takes for an attack to perform an “exhaustive search” to locate a password given the parameters defining the complexity of the underlying password and the method by which it is stored.
An exhaustive search is the maximal time it will take an attacker to find a password for sure given certain parameters. For a simplified version of this function all we need to know are a few simple variables. First we need to know the “character space” of the password. That is, the number of possible character types on the keyboard the password creator may have chosen. For example, if the password is a PIN and is constructed only of numbers then the character space -> C = 10 (as there are 10 decimal numbers 0-9). Lowercase alpha is 26, lower/upper alpha is 52, lower/upper alphanumeric is 62, etc.
The next thing we need to know is the length of the password. In the case of our PIN example above, it may be as short as 4 characters long. In that case we would say that length -> L = 4.
The final thing we want to know is how long does it take to make a single guess. This is where Bcrypt and Scrypt come in. They both attempt to slow down the guessing process by making the time it takes to make a guess longer than other cryptographically secure algorithms. Let’s use a simplified example of relative time… and say that our PIN is stored by way of using SHA256 which hashes in some time T = 1*SHAS for SHAS = the time it takes to run SHA256 on whatever hardware you’re using (this describes the relative nature of these computations against the processing power of the attacker).
In this case, the total time it would take an attacker to guess the PIN 100% for sure is equal to C^L * T = E = 10^4 * 1SHAS = 10000SHAS (with SHAS as relative time value for SHA256 on his hardware… SHAS equaling something small like 1/10^6 second).
The logic behind using Bcrypt or Scrypt to increase the time it takes the attacker to guess the PIN is by an increase in the T value. One way this may be accomplished is by “iterating” a cryptographically secure hashing algorithm against itself. So for example (though this would not be as slow as Bcrypt) let’s follow the same logic and iterate our algorithm 1000 times per run.
Now our T = 1000 and our equation looks like C^L * T = 10^4 * 1000SHAS = 10000000SHAS. This is a significant improvement over the last simulated attack. Now it should take the attacker significantly longer to break the PIN value. By this logic the use of slow hashing algorithms like Bcrypt and Scrypt should be secure, right?
But something is missing. Most specifically, the cost benefit analysis still begs the question, “is the increase in attack difficulty I’m seeing, really worth all the added work?” Remember, this additional work put into the value for T doesn’t just fall on the attacker. Your application must also perform 1000x more work now every single time someone logs in. With a large enough user base, that is no insignificant number.
In fact, as a professional security consultant, I have written reports for companies detailing how their use of Bcrypt could be leveraged by a clever attacker to bring their site offline with ease. Ex. Creating a large number of login events by manipulating profile data.
Give me a real solution…
Thankfully, there is actually a very valid and powerful solution to this issue.
If we look at our exhaustive search function again: C^L * T; using just a bit of college math we can see that there does exist a better solution. Imagine I was to ask you to make the output to this function as large as possible (which is our goal, given that a larger exhaustive search time means more work for the attacker)… Which variable would you want to increase to make the whole product increase the fastest? The Bcrypt and Scrypt folks would tell you that the answer is T. But they’re dead wrong.
It’s L. Given that T > 0, and C > 1; increases to L will cause this function to grow exponentially. Remember L means our length value. We don’t need a large value for T, even a small increase to L will result in a large increase to the total output. All we need is an 8 character PIN and we’ve already exceeded our example “slow hashing algorithm” from earlier. The best part, computationally speaking, increases to L are effectively free. Having your users use longer inputs will not stress your application’s resources.
Now the argument is that it will stress your users. That users need to use shorter passwords that they can remember. For that, I’d like to move the discussion from our inherently simple PIN example, to something a bit more real world.
For the longest time, the recommendation was to use complex passwords. A complex password increases the value C. And certainly there must be at least some minimum value for C given that 1^x = 1 for all x. Practically speaking, we also cannot expect our users to remember passwords of infinite length, so for our equation to grow fast we want at least SOME complexity. But that doesn’t mean you need to be jamming on in l33t speak with some password like $uP3rS1kR##t.
A famous XKCD said it best:
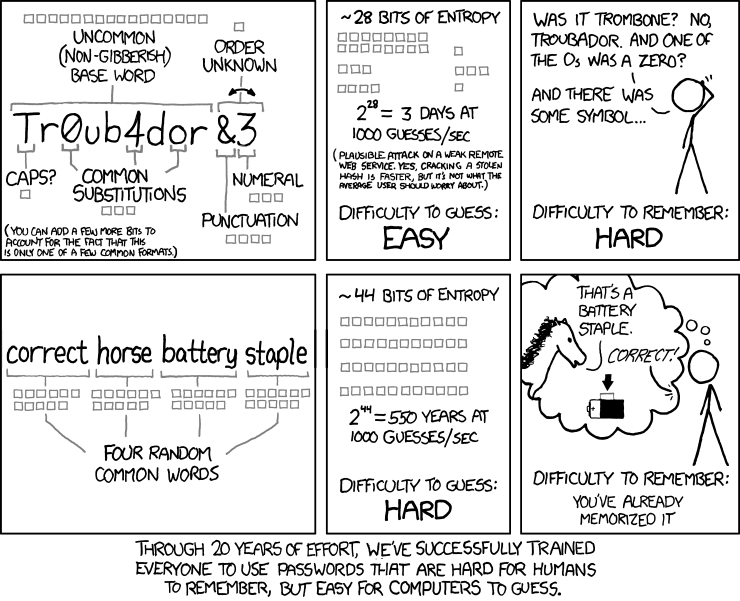
Passphrases give us the ability to easily remember high entropy password values. And rapidly outperform Bcrypt and Scrypt, at no cost to you.
For example, assuming a hashing algorithm that is 210,000x slower than SHA256… and a minimum password length of 10 (which is actually significantly longer than most sites require at this time still, so this is me being wildly generous). Now imagine that someone on this site thought that since the site was using Bcrypt (or whatever) they could have a 10 character password all lowercase alpha. Something like “tunafishgo”. Their E is equal to 26^10 * 210000.
Now imagine another site competing with this one. Simply using SHA256 once, and requiring passphrases. If they use the length of the example passphrase “correcthorsebatterystaple” as per the above… their E is equal to 26^25 * 1.
The raw difference between these two different approaches is that it will take 26^15/210000 ~= 2^53 (SHAS) longer to crack the passphrase site, than it will to crack the passwords protected by our “bcrypt” example. Keep in mind, that this is me being generous, as many sites “secure” their passwords with Bcrypt, then opt for shorter password lengths. I’ve seen lengths as short as 7 in the wild. Additionally, this is done for free by the winning team.. While the Bcrypt camp is out buying more servers just to keep their application running.
In Conclusion
You should not be using Bcrypt. You should be using passphrases. The dangers of Bcrypt and Scrypt are that you will:
– Be lulled into a false sense of security; and actually weaken your passwords
– Waste your resources processing hard algorithms; and lose the real game
One final thought. Of course there must be some sort of minimal difficulty level for the T value as if T = 0 then E = 0 in all cases. It is reasonable to expect that as computers become more powerful, so too should our hashing algorithms. However, as long as you’re using a modern cryptographically secure hashing algorithm like the SHA2 series, with passphrases, your servers, users, and shareholders will all be happier.
“correcthorsebatterystaple” as per the above… their E is equal to 26^25 * 1.
Not true because here you would use a dictionary attack
In a real-world engagement, I cracked an xkcd generated password in 6 days. I am not claiming that all such passwords will fall as easily, but I believe your conclusion to be only partially accurate. The issues of strong password storage and strong password hygiene are not mutually exclusive. (And as can be inferred by my success above, most real-world password cracking does not rely on walking an entire keyspace.)
You misunderstand scrypt. The goal of scrypt is to trade off time and memory, in order to prevent hardware based massively parallel attacks.
If you only have a small amount of memory available per processing core (such as in GPUs), then the time required to perform the calculation is high, since you are forced to continually recalculate intermediate results.
If you have a lot more memory available (such as for a server CPU), you require less time, as you can hold on to the intermediate results.
This ensures that processing requirements are kept low for business as usual activities, but are forced to be high for massively parallel hardware attacks.
The assumption that bcrypt/scrypt will in any way affect the overall performance of the system is flawed. It is only true for poorly designed systems. In the real world, password authentication is only used for initial login and then an alternative mechanism is used for controlling access (JWT, OAuth, etc.). So this argument is flawed.
Secondly, high-performance ASIC hardware for calculating SHA256 is available for very cheap (obsolete bitcoin miners), it is also available for scrypt (scrypt-based cryptocurrency miners) but not for bcrypt. So, this makes anything based on SHA256 vulnerable to brute force attacks by orders of magnitude, while bcrypt is affected the least.
I totally agree that choosing high entropy passwords is way more effective diminishingly small percent of people know the difference and even fewer people know how to use this properly. It is very hard to enforce entropy when creating passwords (tools like zxcvbn are too computationally expensive and there are plenty of other implementations that just doing it wrong), so for foreseeable future we stuck with `John,12345` kind of passwords and the only algorithm that has an edge (and practical) is bcrypt.
I recommend reading https://eprint.iacr.org/2015/387 and in particular the final recommendation. This puts the majority of the hashing work on the client side and the server does very minimal work per user. JS is very powerful these days and very fast so it’s actually a feasible solution.
So this method, in combination with making users use a reasonable length password (14+ chars) and some kind of strength checker to eliminate commonly used dictionary passwords (e.g. zxcvbn), this is a reasonably secure option.
In reality though you probably won’t convince users to use long passwords and passphrases unless you had strict enforcement of it in the code (counting number of words etc). Once you get into passphrase territory and the fact you need a different passphrase per site (in case one is hacked) then it’s really hard for the user to remember them all. Then to solve that you’re going to need to remember one long passphrase (your master passphrase) to unlock your encrypted password database. Once you’re using a password database you may as well just generate random passwords of 30+ chars per site and use copy paste to log in from then on.
Everyone who thinks this is a article with good advice, you’re wrong!
This article is critically flawed. A single iteration of a generic hash function such as SHA2-256 shouldn’t be used for password/passphrase storage. The fact you(the author) assume users will use high-entropy passwords/passphrases is flawed.
To help mitigate the chances of (D)DoS, you must:
* Rate limit authentication attempts.
* Limit the size of data your server accepts.
There isn’t any easy way to mitigate (D)DoS. But using generic hashing algorithms is certainly not the way. Both Bcrypt and Scrypt have parameters that let you adjust how much resources your server consumes. And generally, depending on how large of a user base you have, it’s actually fine to eat up more resources on your server. Most users won’t login more than a couple times a day … most of them save their sessions for long periods of time, so there may be days where your service isn’t even being logged into.
Security experts have been telling everyone not to use fast hashing algorithms for password storage for quite a while now. Your service/database will eventually be broken into, and you think Bcrypt and Scrypt are just toys? They will protect users’ passwords far better than your home-baked solution.
SHA2-256 is very fast to compute. You want it to take as long as possible for someone to guess a password/passphrase. On my old machine, I was able to compute roughly 1,300-ish Bcrypt (with a work factor of 3) hashes per second. With SHA2-256, roughly 100,000-ish. A really big difference.
Note: The standard work factor of a Bcrypt hash is usually 10.
Everyone makes mistakes. I won’t hold you against it, as you simply don’t know any better. I’m worried yet another developer will see your article and take your bad advice.
I highly suggest taking down this article, as there are many people who don’t know any better like yourself. The last thing we need is another database leak of passwords hashed with SHA2-256.
BTW, GitHub is absolutely huge. Guess which algorithm they use to hash our passwords? Bcrypt.
My friend I think I have failed to communicate here. I feel that you are not understanding what I have tried to say here, and I want to take responsibility for that. If you would please consider reviewing the article again, my intention is to show how a better formulation can be created without the use of bcrypt or scrypt. What I show is correct though I know it is hard to explain. Bcrypt or scrypt do add some value, but I think it is very little value, and what is better is to require long passwords… this is shown mathematically to be harder to crack!
To enforce length of passwords without the poor UX, most applications these days just generate a cryptographic salt, which essentially appends random fixed-length strings to the end of passwords before they are put through the hashing function. This prevents lookup or rainbow table attacks.
Storing passwords in plaintext anywhere is a dangerous and unethical practice. Developers, sysadmins and other people with privileged access should not be able to read user’s passwords. The goal of the hash is that even if your database is leaked, accessed by a bad guy, or someone internal is social engineered to share information, no one can read that password. As a security consultant, you should absolutely urge your clients to hash their passwords. As a user, you should be happy that most good applications and companies are responsible enough to cryptographically hash and salt your passwords so that their employees can’t read them. Would anyone with the slightest to lose willingly create an account in a financial services application if they knew their password would be stored in plaintext?
IMHO you should be using a long random password *and* an expensive algorithm such as Bcrypt (and two factor authentication).
– A passphrase composed of actual words has much less entropy than a *random* passphrase of the same length, they are not directly comparable.
– Using a password manager solves the problem of users having to remember things (and has other benefits, such as making it more difficult for users to share passwords).
– DOS attacks against logins can be frustrated by limiting the number of unsuccessful attempts allowed before lockout, and adding a delay before the next attempt will be processed.
– Computation costs for legit users logging into their accounts are pretty small, really. Unless you are Facebook, in which case you can afford it.
Not using a slow hash is a particular horror if the attacker gets their hands on the user table and can mount a fast offline attack on the hashes. This scenario is the main reason for choosing a slow hash.
Even if you use a slow hash, aren’t you simply delaying the inevitable? In the scenario where someone has an offline copy of your user table, it’s game over surely.
Facebook uses scrypt and has the largest user base in the world
Sorry if this question is lame or naive, but what if I bcrypt a high entropy password?
So – instead of using “Tr0bador&3” as my password, but rather use “correct horse battery staple” and store that password as a bcrypted hash with a cost of 10?
Once again – if I am misunderstanding the difference between the actual password and how it is encrypted, I apologize.
No this is a good question. If you have a strong password which is passed through a slow hashing algo like bcrypt, it will be even harder to crack. However in this case most of the difficulty for an attacker comes from how strong your password is, and only a little comes from bycrypt. Does that make sense?
it would be good to be more specific about the costs to the server – in AWS, how much would it cost per day, if you have e.g. 10k logins per day? And how high would be the typical server cost for keeping up with this number of users, if bcrypt or scrypt weren’t used?
My guess is that the extra cost will be negligible.
But if we had those numbers, then we will be in a good position to examine the trade-off between forcing users to remember more complex password vs using extra processing time.
A lot of people have a bad memory, and can’t remember harder passwords very well.
I believe your argument to use passphrases instead of scrypt or bcrypt is flawed because the use of passphrases is a decision the user makes while the use of scrypt or bcrypt is a decision the server makes. A secure system will do extra work to protect users and that extra cost is of value to your users.
Perhaps I could rephrase to emphasize what I mean here, but you can enforce passphrases by increasing length of pass requirements!
The conclusion “You should not be using Bcrypt. You should be using passphrases.” is a fallacious syllogism. The “You” in the first statement is a developer as the end user does not use Bcrypt or is even aware of password hashing. The “You” in the second statement is an end user as users pick their passwords. So, just because users *should* use better passwords doesn’t imply developers should not use Bcrypt. On the other hand, if a system enforces high password length and uses something like zxcvbn to encourage stronger passwords, it may be reasonable to use fewer iterations.
Does your analysis take into account salting and peppering the user password? I don’t really understand the focus on the L value since the user’s password length is effectively unimportant since it’s combined with a salt (and possibly a pepper).
A salt doesn’t protect against a brute force attack, it only protects against precomputed hash tables. A pepper can help stop an attacker from ever being able to launch a brute force attack, and I do recommend peppering, but the L value is still important in case the pepper is compromised.
Great article and following comment discussion. I’m glad this is on the web. I’ll be walking away with the feeling that long (and possibly strong) passwords enforced by the UI, *plus* a strong (high work) hashing algorithm like bcrypt/scrypt is the ticket. (…with considerations for mitigating DOS during login and tweaking the hash work levels based on number of logins expected per hour.)